O matemático e advogado francês Pierre de Fermat estudou o cálculo dos máximos e mínimos para as funções do tipo y = x ^ n, e esse estudo acabou levando ao problema da reta tangente. Com a ajuda de Mersenne, os resultados se espalharam e, em meados da década de 1630, Fermat e Descartes foram alguns dos pioneiros na busca de tangentes para gráficos. Fermat é conhecido por ser a melhor maneira de testar o desempenho dos processadores de computador com o Último Teorema de Fermat e Mersennes Cousins.
Inicialmente, eles trabalhavam com métodos mecânicos. A teoria de Descartes foi baseada no uso de curvas auxiliares, isto é, mais geométrica que algébrica. Depois disso, Sluse e Hude desenvolveram técnicas mais avançadas, mas geralmente não resolveram o problema. Leibniz e Newton foram os primeiros a desenvolver técnicas que pudessem resolver o problema de funções genéricas. A equação da reta tangente ao gráfico da função y = f (x) no ponto (a, b) é y-b = f ‘(a) (x-a). Este resultado é dado simplesmente pela equação de uma linha na qual um ponto e uma inclinação são conhecidos.

A derivada da função em um ponto é apenas a inclinação da tangente nessa posição. O problema da reta tangente está originalmente relacionado à questão de determinar a velocidade instantânea de um móvel. A velocidade média é a inclinação da reta secante. Portanto, é suficiente reduzir o intervalo de tempo mais e mais para obter a velocidade em um momento.
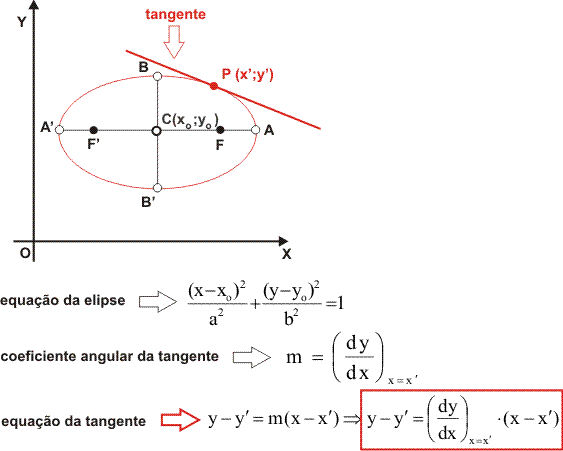
As posições de uma reta em relação a um círculo mostram três possibilidades para essas posições, todas dependendo da distância do centro da circunferência à reta. Para entender melhor o que é abordado neste artigo, indicamos como os artigos são lidos. Distância entre ponto e linha e posição relativa entre uma linha e um círculo. Encontramos a tangente a partir de um ponto cuja posição é de grande importância para o estudo da tangente. Portanto, teremos os seguintes casos:
• Ponto P dentro da circunferência (distância do centro a um ponto menor que o raio), não há tangente sob estas condições;
• O ponto P como um ponto na circunferência (distância do centro ao ponto correspondente ao raio) nos dá uma única tangente, onde P é o ponto de tangência.
• ponto P fora da circunferência (distância do centro ao ponto que é maior que o raio), através deste ponto duas tangentes são guiadas. Portanto, antes de procurarmos a linha tangente, precisamos verificar a posição relativa entre o ponto e o perímetro.

Vamos ver um exemplo:
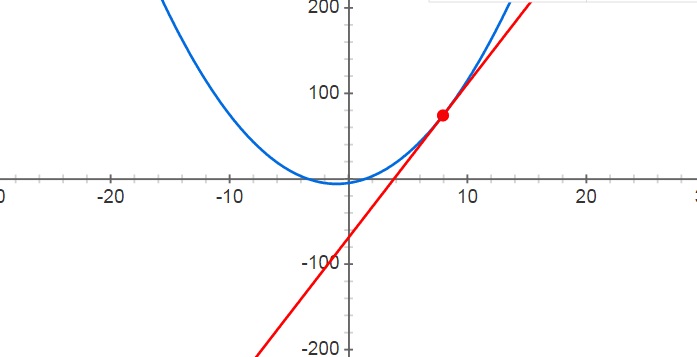
Determine as equações das linhas tangentes à circunferência λ: x² + y² = 1, representadas pelo ponto P (√2, 0). Devemos verificar a posição relativa ao escopo. Então, calcule a distância deste ponto até o centro da circunferência. Este círculo tem o centro C (0,0) e o raio r = 1. Portanto:
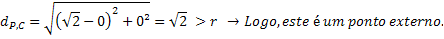
Se o ponto P é um ponto externo, podemos dizer que temos que encontrar duas tangentes. Se as linhas forem tangentes, sabemos que a distância do centro até a linha tangencial deve ser igual ao raio. Essa tangente deve passar pelo ponto P (√2, 0). A equação da linha t é assim: t: y-0 = m (x-√2) -> mx-y-√2m = 0 A equação da linha nos permite calcular a distância do centro da circunferência à tangente.

Nós simplesmente substituímos o valor do coeficiente angular m na equação de nossa tangente para obter a resposta final.
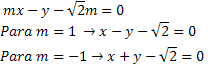
Para encontrar a equação de uma linha tangente desenhada por um ponto particular, é necessário conhecer a posição relativa desse ponto para analisar o comportamento da linha que passa por esse ponto e a tangência da circunferência.
A aplicação atual do cálculo da tangente está no campo econômico. Alguma pesquisa sobre a elasticidade da procura procura uma linha reta através da origem. Os pontos máximo e mínimo de uma função ocorrem quando a tangente tem um declive (linha horizontal) ou se ela não existe. Assim, os problemas da tangente e do máximo e mínimo estão relacionados.
Em contraste com a linha reta, a inclinação de uma curva muda constantemente conforme se move ao longo do gráfico. Cálculo apresenta aos alunos o conceito de que qualquer ponto desse gráfico pode ser descrito como uma inclinação ou “taxa instantânea de mudança”. A tangente é uma linha reta relativa a essa inclinação que passa pelo mesmo ponto no diagrama. Para descobrir qual é a equação tangente, você precisa saber como extrair a derivada da equação original.
Para entender o conceito de derivação, você deve primeiro saber o que é uma tangente. Nós fixamos um ponto P no gráfico de uma função f e escolhemos um Q ≠ P. Quando Q é introduzido em P, pode acontecer que a linha PQ tenha uma posição final: uma linha t. Nesse caso, t é chamado de tangente de f em P, a menos que seja vertical. Portanto, a linha PQ é chamada de linha secante para o gráfico de f em P. No diagrama abaixo, vemos que Q deve se aproximar de P tanto para a esquerda quanto para a direita, e em ambos os casos a linha reta PQ tende a t (linha verde).
Primeiro gráfico – Pela esquerda
Segundo gráfico – Pela direita
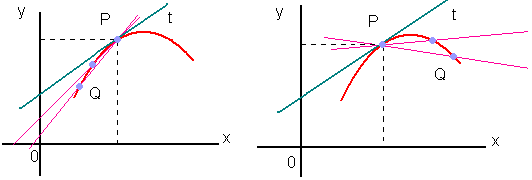
OBS: A reta tangente ao gráfico de uma função que nem sempre existe.
A figura abaixo apresenta um exemplo de gráfico onde P é o bico de uma função, assim sendo, o processo descrito anteriormente conduz a duas posições-limites (t1 e t2), obtidas respectivamente ao fazer Q se aproximar de P pela esquerda e pela direita.
Cálculo da inclinação da tangente
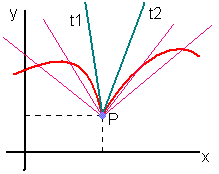
Considere a curva que é o gráfico de uma função contínua f e P (xo, f (xo)) de um ponto na curva. Vamos agora analisar a inclinação (coeficiente angular) da tangente à curva traçada em f no ponto P.
Para analisar isso, escolhemos um pequeno número Δ x que é diferente de 0, onde Δ x é o deslocamento no eixo das abcissas. No gráfico marcamos o ponto Q (xo + Δ x, f (xo + Δ x)). Nós desenhamos uma linha secante através dos pontos P e Q.
A inclinação (coeficiente angular) desta linha é dada da seguinte forma:
Exercícios de Equação da Reta Tangente




exercício 6