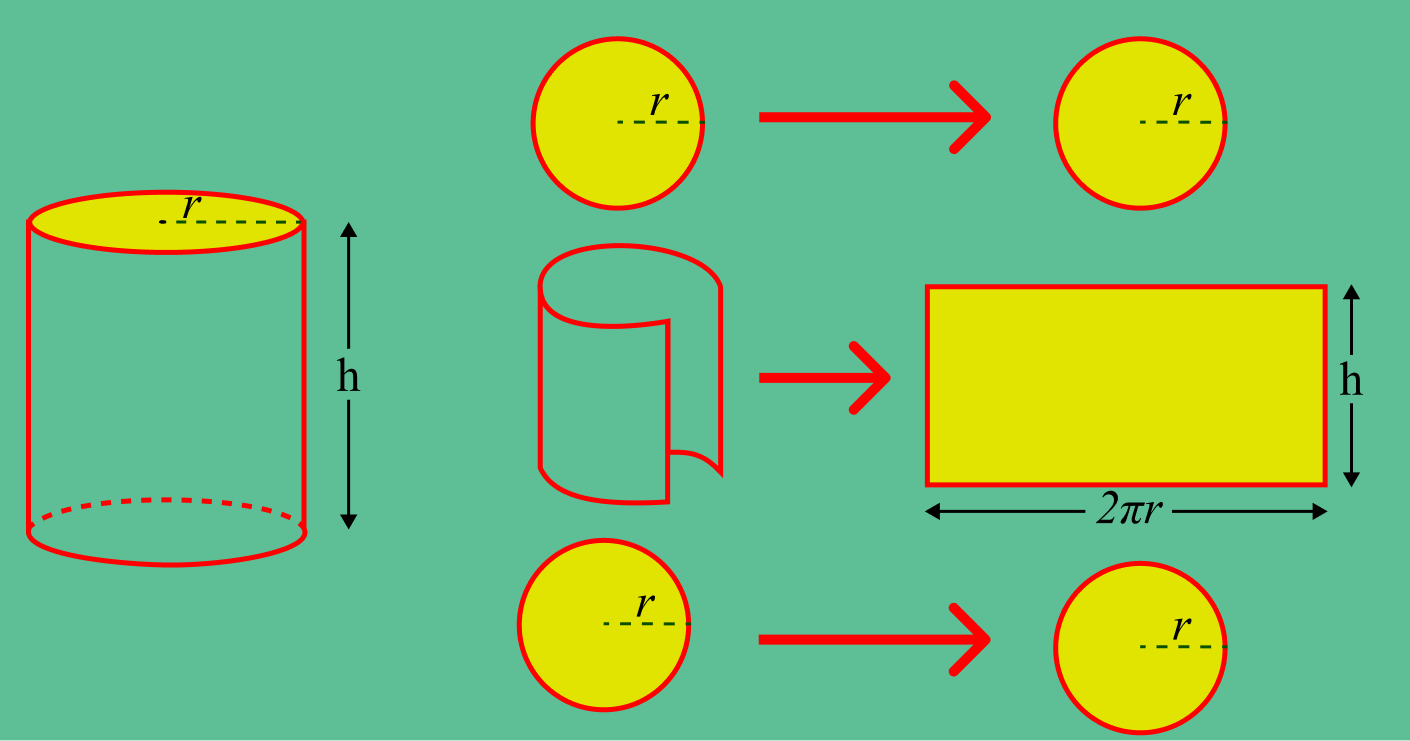
O cilindro trata-se de um corpo geométrico, em onde todos os segmentos de linha são paralelos, começando em qualquer plano de um círculo e terminando em outro plano paralelo ao primeiro plano. O cilindro ou cilindro circular é um corpo geométrico alongado e arredondado com o mesmo diâmetro em todo o seu comprimento.
Um cilindro é um objeto tridimensional com duas bases planas redondas e um lado curvo. Tem uma superfície curva no meio. A base e a superfície superior são idênticas. Isso significa que as bases são sempre paralelas e congruentes entre si. Não tem vértices.

Agora, se olharmos para esta figura com cuidado, vemos que há três faces do cilindro. Dois círculos e um retângulo. Um círculo está na base do cilindro e outro no topo. Ambos os círculos são do mesmo tamanho. A face retangular é a superfície curva do cilindro. Assim,
- A área do círculo do cilindro é πr².
- A área de dois círculos será de 2πr².
- O raio ‘r’ de um cilindro é o raio de sua base. Agora, a área do retângulo = comprimento x largura. 2πr é a circunferência do círculo e h é a altura. Área da superfície curva será = 2πr × h = 2πrh
Então a área do cilindro será: 2πr² + 2πrh, ou
Área de Superfície Total do Cilindro = 2πr (r + h)
Onde r é o raio eh é a altura do cilindro (a distância entre as duas bases).
O Volume de um Cilindro
Suponha que se temos um cilindro de raio r e altura h, então o volume será,
V = πr²h
V é a quantidade de espaço ocupada pelo objeto tridimensional. Vamos ver um exemplo para descobrir o volume de um cilindro. Como sabemos, π = 3,14. Então, vamos encontrar o volume de um cilindro que tenha o raio de 3 cm e a altura de 5 cm. Agora,
V = πr²h
= π (3²) 5
= π (9) 5
= (
3,14 ) (45) = 141,30 cm³
Na matemática, chamamos os cilindros de objetos tridimensionais, oblongos e redondos, com o mesmo diâmetro em todo o seu comprimento. Pode-se dizer que o cilindro também pode ser definido por uma área quadrada cuja função geradora é:
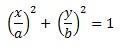
Quando o cilindro é circular, “a” e “b” têm o mesmo valor na equação acima. Cilindros circulares também podem ser chamados de cilindros equilaterais. Isso acontece quando a altura é igual ao diâmetro da base.
Chamamos de geratriz todos os segmentos retos que são paralelos ao eixo do cilindro e têm as extremidades nas bases.
Eixo é o segmento reto com as extremidades no meio da base do cilindro.
A altura de um cilindro circular é a distância entre os círculos planos das bases. Os cilindros podem ser retos, circulares ou obliquamente circulares. No primeiro caso, o eixo e as geratrizes são perpendiculares às bases e congruentes com sua altura. (FIGURA A) No segundo caso, o eixo e as geratrizes são oblíquos aos planos da base e não congruentes com sua altura. (FIGURA B)
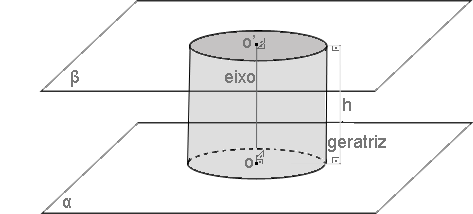
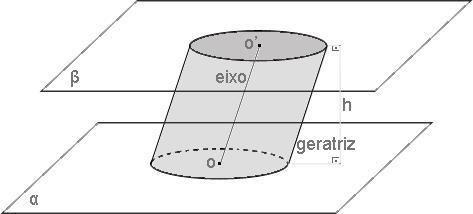
Esta figura geométrica integra os estudos de geometria espacial e apresenta dois círculos com raios de medidas equivalentes os quais estão situados em planos paralelos.
O cálculo da superfície cilíndrica é semelhante ao cálculo da superfície do prisma.
Este cálculo é feito em três etapas: área de base, área lateral e soma das duas últimas. Antes de entrar em exemplos, é importante entender bem o que é um cilindro e algumas de suas características básicas. O resultado dessa configuração pode ser visto na figura a seguir:
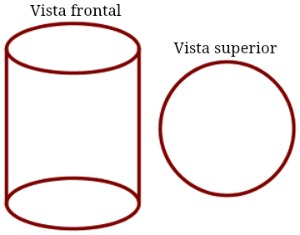
À esquerda na figura está um cilindro da frente e do lado direito, o mesmo cilindro pode ser visto de cima. O cilindro consiste em dois círculos e o volume total entre esses círculos. O desenho do cilindro tem exatamente a forma de um retângulo ou paralelogramo quando o cilindro é oblíquo e duas circunferências.
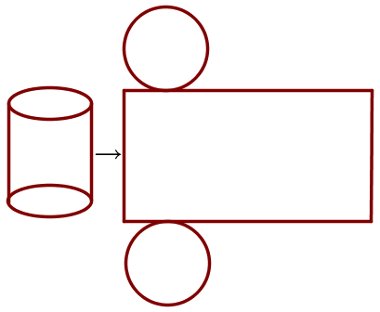
Confira um exemplo de exercício de cálculo da área e volume do cilindro:

Quais São os Componentes do Cilindro?
- Raio: distância entre o centro do cilindro e a extremidade.
- Base: plano que contém a diretriz e no caso dos cilindros são duas bases (superior e inferior).
- Geratriz: corresponde à altura (h=g) do cilindro.
- Diretriz: corresponde à curva do plano da base.
Como os Cilindros São Classificados?
Dependendo da inclinação do eixo, ou seja, o ângulo formado pela geratriz, os cilindros são divididos nas seguintes classes:
Cilindro reto: Para os cilindros retos, o gerador (altura) é perpendicular ao plano da base.
Cilindro oblíquo: Para cilindros circulares oblíquos, a geratriz (altura) é oblíqua em relação ao plano da base.
O chamado “cilindro equilateral” ou “cilindro rotativo” é caracterizado pela mesma medida do diâmetro da base e da geratriz (g = 2r). Isso ocorre porque a seção do meridiano corresponde a um quadrado. Para ampliar seu conhecimento sobre esse tópico, veja outras figuras que fazem parte da geometria do espaço.

Quais São as Fórmulas do Cilindro?
Aqui estão as fórmulas para calcular superfícies e volumes de cilindros:
Áreas do Cilindro
Área da Base: A fórmula a seguir é usada para calcular a área da base do cilindro:
Ab = π.r2
Onde:
Ab: área da base
π (Pi): 3,14
r: raio
Área Lateral: Para calcular a área lateral do cilindro, ou seja, a medida da superfície lateral, é utilizada a fórmula:
Al= 2 π.r.h
Onde:
Al: área lateral
π (Pi): 3,14
r: raio
h: altura
Área Total: Para calcular a área total do cilindro, ou seja, a medida total da superfície da figura, soma-se 2 vezes a área da base à área lateral, a saber:
At= 2.Ab+Al ou At = 2(π.r2) + 2(π.r.h)
Onde:
At: área total
Ab: área da base
Al: área lateral
π (Pi): 3,14
r: raio
h: altura

Volume do Cilindro
Calcula-se o volume do cilindro a partir do produto da área da base pela altura (geratriz):
V = Ab.h ou V = π.r2.h
Onde:
V: volume
Ab: área da base
π (Pi): 3,14
r: raio
h: altura
Exemplos Resolvidos
1- Que comprimento de um cilindro sólido de 2 cm de diâmetro deve ser recolocado em um cilindro oco de diâmetro externo de 20 cm, 0,25 cm de espessura e 15 cm de comprimento?
a- 54,06 cm
b- 74,06 cm
c- 34,06 cm
d- 64,06 cm
Solução: B. O diâmetro do cilindro sólido = 2 cm ou o raio = 1 cm; altura h =?
V 1 = πr²h = π (1) ²h = πh
Para o cilindro oco, H = 15 cm; diâmetro externo = 20 cm ou raio externo = 10 cm. Portanto, diâmetro interno = 10-0,25 (espessura + = 9,75 cm. Portanto,
V 2 = π [10² – (9,75²)] × 15 = 15π × 19,75 × 0,25
Além disso, V 1 = V 2 , que dá
h = 74,06 cm
2- Se a superfície lateral do cilindro for de 500 cm² e sua altura for de 10 cm, encontre o raio de sua base:
a – 7,96 m
b – 7,96 cm
c- 7,96 cm²
d – 9,61 cm²
Solução: B. A área da superfície lateral é A = 2πrh. A área de superfície curva é A = 500 cm² e sua altura é de 10 cm, portanto
A = 2πrh
500 = 2 × 3,14 × 10 ×
500 = 62,8r
r = 500 / 62,8
= 7,96
Portanto, o raio do cilindro é de 7,96 cm